Distribuições de probabilidade

Entenda mais sobre distribuições de probabilidade com as linguagens R e Python.

Bibliotecas necessárias:

Python

Código

import pandas as pd
import numpy as np
import scipy.stats as stats
from scipy.stats import expon
from scipy.stats import t
from scipy.stats import f 
import plotly.express as px
import seaborn as sns
import matplotlib.pyplot as plt

R

Código

library(dplyr, warn.conflicts=FALSE)
library(tidyverse, warn.conflicts=FALSE)
library(reticulate, warn.conflicts=FALSE)

Distribuições de Probabilidade

Uma distribuição de probabilidade descreve como os valores de uma variável aleatória são distribuídos. Por exemplo, sabe-se que a coleção de todos os resultados possíveis de uma sequência de lançamento de moedas seguem a distribuição binomial. Já as médias de amostras suficientemente grandes de resultados de lançamentos de dados se assemelham à distribuição normal. Como as características dessas distribuições teóricas são bem compreendidas, elas podem ser usadas para fazer inferências estatísticas em toda a população de dados.

A seguir, destrincharemos algumas das distribuições mais usadas, e como obter probabilidades usando Python e R.

Binomial

Usada em casos de experimentos repetidos, onde existem dois possíveis resultados: fracasso ou sucesso. Assim, em n tentativas independentes de um experimento, cada uma tem probabilidade de sucesso p e probabilidade de fracasso 1-p.

A probabilidade de alcançar r fracassos em n elementos da amostra:

\[ \frac{n !}{(n-r) ! * r !} \]

Assim, a função de massa de probabilidade (pmf) , que é a probabilidade total de alcançar r fracassos em n elementos da amostra:

\[ \frac{n !}{(n-r) ! * r !} * p^r *(1-p)^{n-r} \]

Exemplo: Para calcular a probabilidade de obter 8 caras, a partir de um experimento com 20 tentativas, em que a probabilidade de se obter uma cara em qualquer tentativa é 0.5:

Python

No Python, podemos usar a função “binom.pmf”, onde pmf quer dizer “probability mass function”, da biblioteca SciPy para obter a probabilidade desejada. Os argumentos passados para a função primeiro número de sucessos (8), número de tentativas (20) e por fim a probabilidade de sucesso (0.5).

Conforme abaixo:

Código

stats.binom.pmf(8, 20, 0.5)

0.1201343536376954

Criamos um dataframe pandas com as probabilidades de sucesso, de 1 a 20. Após, usamos este dataframe para plotar a distribuição de probabilidade deste caso.

Código

n = 20
p = 0.5
lista_probs=[]
n_sucessos=[]

for i in range(1,n+1):
    prob=stats.binom.pmf(i, 20, 0.5)
    lista_probs.append(prob)
    n_sucessos.append(i)

data = {'Sucessos':n_sucessos,'Probabilidade':lista_probs}
df = pd.DataFrame(data)

fig = px.line(df, x='Sucessos', y='Probabilidade', markers=True,template='ggplot2',title='<b> Distribuição Binomial: n=20, p=0.5')
fig.show()

R

No R, a função usada para obter a probabilidade desejada é a “dbinom”. Os argumentos no caso do exemplo serão: x=4 | size=20 | prob=0.5

Conforme abaixo:

Código

dbinom(x = 8, size = 20, prob = 0.5)

[1] 0.1201344

A seguir, criamos uma tabela com as probabilidades de sucesso, de 1 a 20. Após, usamos esta tabela para plotar a distribuição de probabilidade deste caso.

Código

n = 20
p = 0.5
binom_prob <- tibble(n_success = 1:n) %>%
  mutate(prob = dbinom(n_success, size=n, prob=p))

binom_prob %>%
  ggplot(aes(x=n_success, y=prob))+
  geom_line()+
  geom_point(size=2)+
  scale_x_continuous(breaks=1:n)+
  scale_y_continuous(breaks = scales::pretty_breaks(n = 5))+
  labs(x= "Número de sucessos",
       y= "Probabilidade",
       title=paste0("Distribuição Binomial: n=20, p=0.5"))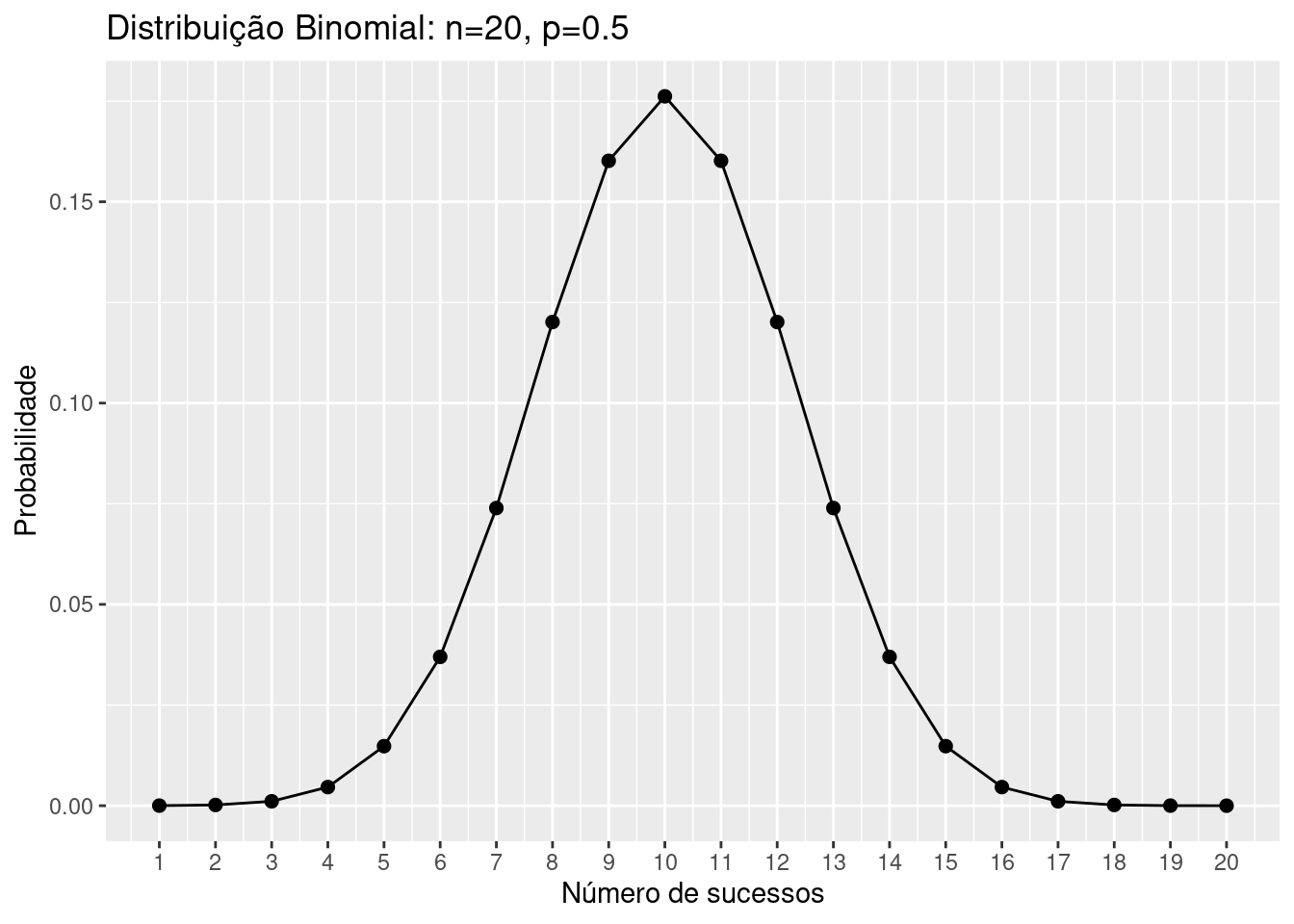

Cada distribuição de probabilidade em R está associada a quatro funções que seguem uma convenção de nomenclatura:

• A função de densidade de probabilidade sempre começa com ‘d’;

• A função de distribuição cumulativa sempre começa com ‘p’;

• A função quantílica sempre sendo com ‘q’;

• E uma função que produz variáveis aleatórias sempre começa com ‘r’.

Cada função recebe um único argumento para avaliar a função, seguido por parâmetros específicos que definem a função de distribuição específica a ser avaliada.

Poisson

A Distribuição Poisson modela a probabilidade de eventos ocorrerem em um período fixo de tempo, ou seja, aqui contamos eventos que ocorrem aleatoriamente, mas a uma taxa média definida.

Exemplo: Em uma indústria, há a ocorrência de cerca de 7 ítens defeituosos por dia. Encontre a probabilidade de que, em um dia, 10 ítens apresentem defeito:

Python

No Python, podemos usar a função “poisson.pmf”, para obter a probabilidade desejada. O primeiro argumento que passamos para a função é o 10 (queremos saber a probabilidade de observar exatamente 10 ítens defeituosos) e a taxa de defeitos por dia, que é 7. Conforme abaixo:

Código

stats.poisson.pmf(10, 7)

0.07098326865041356

Criamos um dataframe pandas com as probabilidades de ítens defeituosos, de 1 a 15. Após, usamos este dataframe para plotar a distribuição de probabilidade deste caso.

Código

n = 15
lista_probs=[]
n_prob=[]

for i in range(1,n+1):
    prob=stats.poisson.pmf(i, 7)
    lista_probs.append(prob)
    n_prob.append(i)

data = {'Defeitos':n_prob,'Probabilidade':lista_probs}
df = pd.DataFrame(data)

fig = px.line(df, x='Defeitos', y='Probabilidade', markers=True,template='ggplot2',title='<b> Distribuição Poisson: lambda = 7')
fig.show()

R

No R, a função usada para obter a probabilidade desejada é a “dpois”. Os argumentos no caso do exemplo serão 10 e 7.

Conforme abaixo:

Código

dpois(10, 7)

[1] 0.07098327

Novamente, como na saída em Python, encontramos a probabilidade de cerca de 7%.

A seguir, criamos uma tabela com as probabilidades de ítens defeituosos, de 1 a 15. Após, usamos esta tabela para plotar a distribuição de probabilidade deste caso.

Código

n = 15
pois_prob <- tibble(n = 1:n) %>%
  mutate(prob = dpois(n, 7))

pois_prob %>%
  ggplot(aes(x=n, y=prob))+
  geom_line()+
  geom_point(size=2)+
  scale_x_continuous(breaks=1:n)+
  scale_y_continuous(breaks = scales::pretty_breaks(n = 5))+
  labs(x= "Defeitos",
       y= "Probabilidade",
       title=paste0("Distribuição Poisson: lambda = 7"))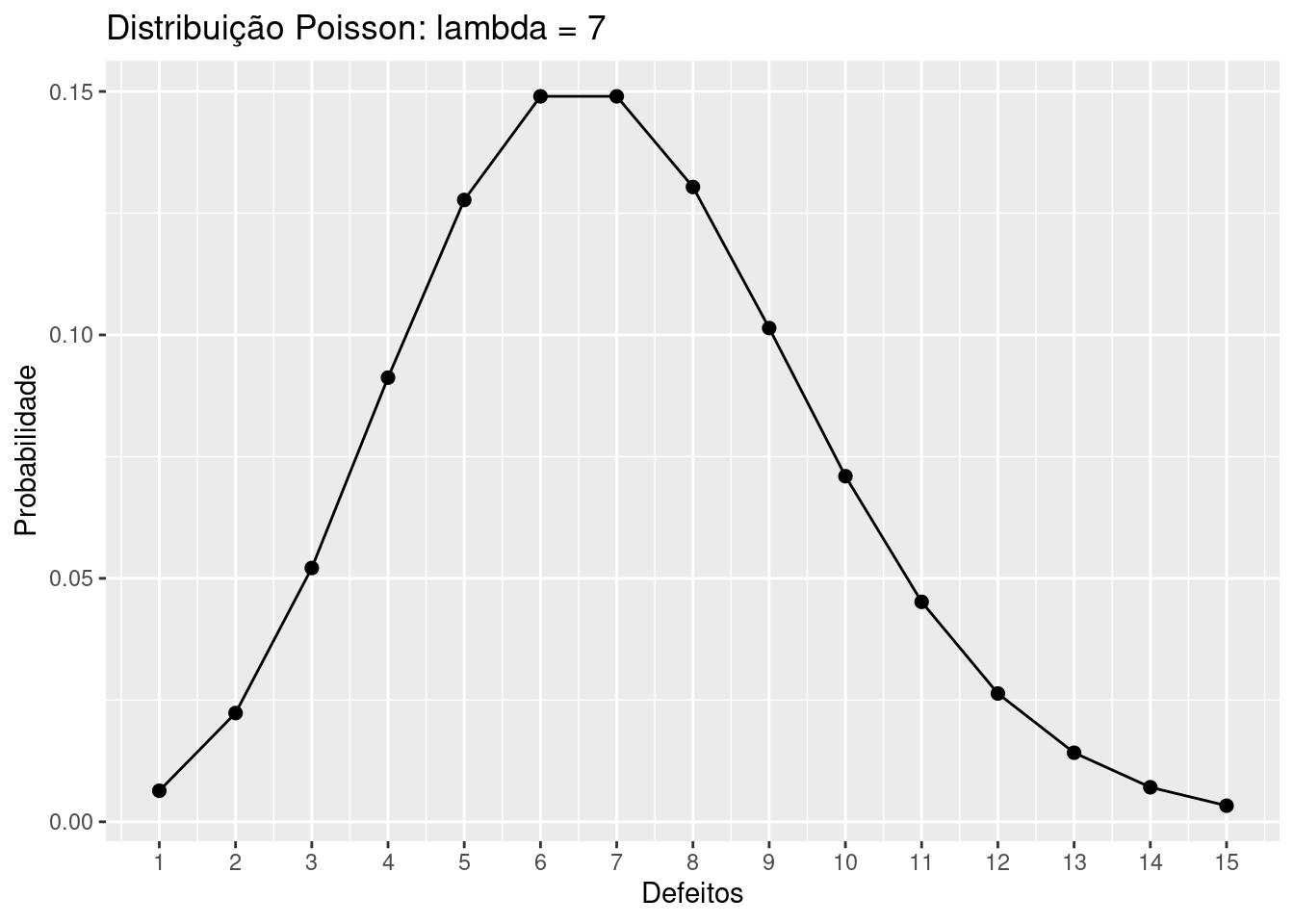

Normal

Muitas variáveis ​​nas ciências naturais e sociais têm distribuição normal ou aproximadamente normal. Alguns exemplos são altura, peso ao nascer, satisfação no trabalho, dentre muitas outras.

Compreender as propriedades das distribuições normaisnos ajuda a usar estatísticas inferenciais para comparar diferentes grupos e fazer estimativas sobre populações usando amostras.

Características da distribuição normal:

• A média, a mediana e a moda são exatamente iguais;

• A distribuição é simétrica em relação à média – metade dos valores ficam abaixo da média e metade acima da média;

• A distribuição pode ser descrita por dois valores: a média e o desvio padrão.

Outras características importantes:

• Cerca de 68% dos valores estão dentro de 1 desvio padrão da média;

• Cerca de 95% dos valores estão dentro de 2 desvios padrão da média;

• Cerca de 99,7% dos valores estão dentro de 3 desvios padrão da média.

Função densidade de probabilidade:

\[ f(x)=\frac{\exp \left(-x^2 / 2\right)}{\sqrt{2 \pi}} \]

Python

Em Python, usamos a função “norm.pdf”, para obter a distribuição desejada. Primeiro, criamos uma amostra de intervalo [-5, 5], de 0.01 em 0.01. Após, passamos para a função “norm.pdf” os parâmetros amostra, média e variância, no exemplo abaixo 0 e 1 respectivamente, conforme pode ser visto:

Código

amostra = np.arange(-5, 5, 0.01)
probs = stats.norm.pdf(amostra, 0, 1)
data = {'Valor':amostra,'Probabilidade':probs}
df_normal = pd.DataFrame(data)

fig = px.line(df_normal, 'Valor', 'Probabilidade',template='ggplot2')
fig.update_layout(title_text='Distribuição Normal')

Podemos estar interessados em descobrir o valor de um quantil específico. Para descobrirmos o quantil 0.75, por exemplo, podemos fazer como abaixo:

Código

df_normal['Valor'].quantile(0.75)

2.4924999999998403

Que corresponde ao valor 2.49.

R

Código

pnorm(q = 100, mean=72, sd=15.2, lower.tail=FALSE) 

[1] 0.03272988

Código

dnorm( x=80, mean=60, sd=15 )

[1] 0.010934

Código

qnorm( p=0.75, mean=80, sd=16 )

[1] 90.79184

Código

out <- seq(-9, 9, length=100)
prob <- dnorm(out)
media <- c(0, -1, 2)
dp <- c(1, 2, 3)

colors <- c("red", "blue", "darkgreen")
labels <- c("mean = 0, sd = 1", "mean = -1, sd = 2", "mean = 2, sd = 3")
colors <- c("red", "blue", "darkgreen")

plot(
  out, prob, type="l", lty=2, xlab="x value",
  ylab="Density", main="Comparison of Normal Distributions",
  frame.plot=FALSE
)

for (i in 1:3){
  lines(out, dnorm(x = out, mean = media[i], sd = dp[i]), lwd=2, col=colors[i])
}


legend("topright", inset=.05, title="Distributions",
  labels, lwd=2, lty=c(1, 1, 1), col=colors)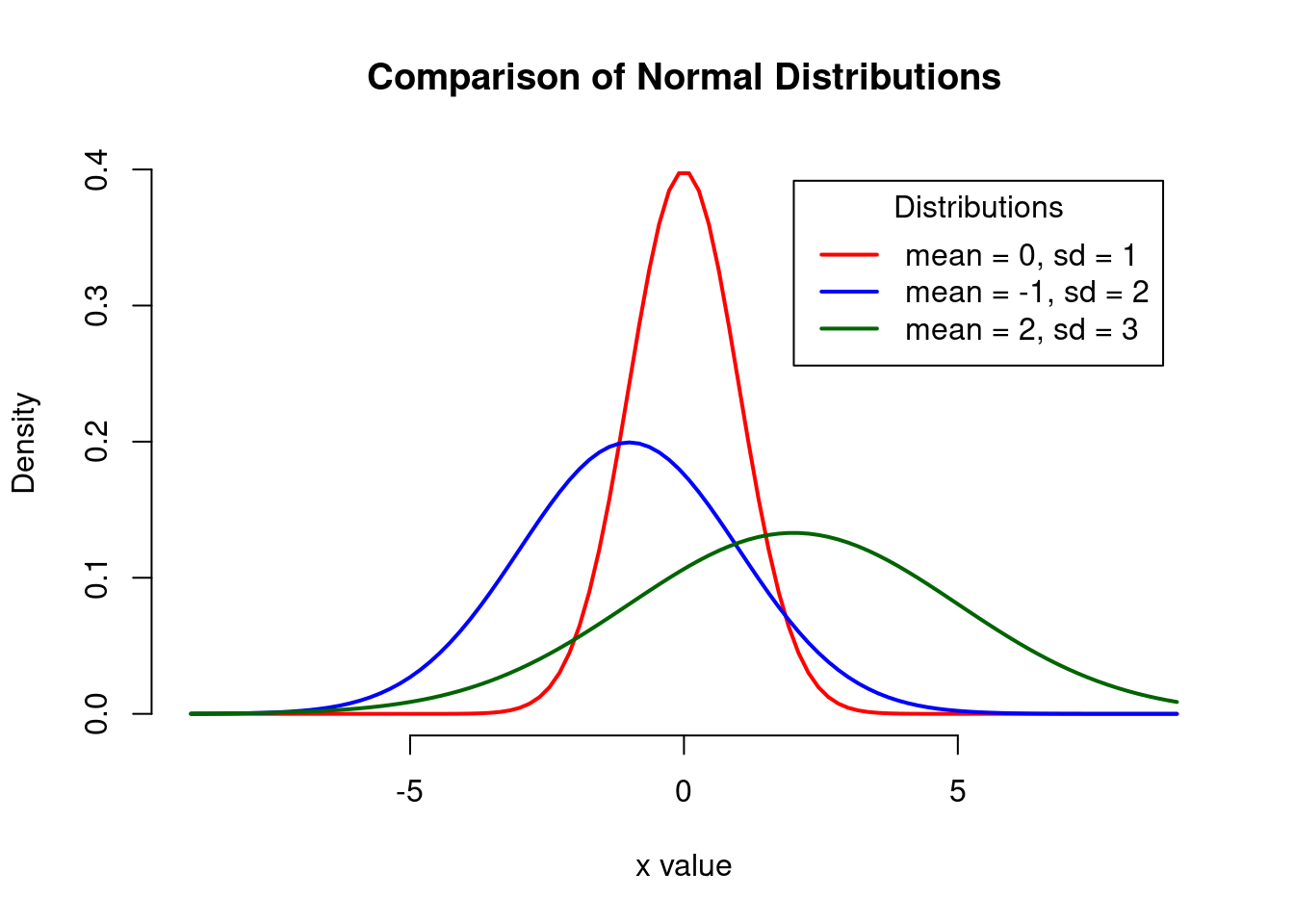

Uniforme

A distribuição uniforme refere-se a um tipo de distribuição de probabilidade em que todos os resultados são igualmente prováveis.

Como exemplo, poderíamos pensar na probabilidade de tirarmos de 1 a 6, ao lançarmos um dado. A probabilidade de qualquer dos resultados é de 1/6.

Python

Código

probs = np.full((6), 1/6)
face = [1,2,3,4,5,6]
axes = plt.gca()
axes.set_ylim([0,1])

(0.0, 1.0)

Código

plt.bar(face, probs)
plt.ylabel('Probabilidade', fontsize=12)
plt.xlabel('Resultado do lançamento de dados', fontsize=12)
plt.title('Distribuição uniforme de dados justos', fontsize=12)

R

Código

punif(0.75, min=0, max=10 )

[1] 0,075

Código

dunif( 0.5, min=0, max=10 )

[1] 0,1

Código

qunif( 0.5, min=0, max=4, lower.tail=T )

[1] 2

Código

x <- seq(-4, 4, length=100)

y <- dunif(x, min = -3, max = 3)

plot(
  x, y, type='h', lwd=3, ylab="Probability",
  frame.plot=FALSE, col=4
)

Exponencial

A distribuição exponencial é uma distribuição de probabilidade que é usada para modelar o tempo que devemos esperar até que um determinado evento ocorra.

Python

Para gerar uma amostra exponencial, em Python, usamos a função “expon.rvs” da biblioteca SciPy. Abaixo, como exemplo, geramos uma amostra de tamanho 10, e taxa média 40.

Código

exp_amostra=expon.rvs(scale=40, size=10)
exp_amostra

array([  9.02275607,  23.26908466,   8.91749082,  50.87741258,
       107.57208417,  52.01864752,  11.14855552, 143.59986616,
         3.62098063,  58.03659311])

Para encontramos, por exemplo, a probabilidade de que x seja menor que 50 quando a taxa média for 40, podemos usar a função “expon.cdf”, conforme abaixo:

Código

expon.cdf(x=50, scale=40) 

0.7134952031398099

Que nos mostra uma probabilidade de cerca de 71%.

Abaixo, plotamos a distribuição de uma amostra de tamanho 250. O eixo y mostra a probabilidade daquele número de ocorrências. Mantivemos a taxa média em 40.

Código

n = 250
lista_probs=[]
n_prob=[]

for i in range(1,n+1):
  prob=expon.pdf(i, scale=40) 
  lista_probs.append(prob)
  n_prob.append(i)

data = {'n':n_prob,'Probabilidade':lista_probs}
df = pd.DataFrame(data)

fig = px.line(df, x='n', y='Probabilidade', markers=True,template='ggplot2',title='<b> Distribuição Exponencial: lambda = 40')
fig.show()

A distribuição acumulada para o exemplo ficaria como abaixo:

Código

n = 250
lista_probs=[]
n_prob=[]

for i in range(1,n+1):
  prob=expon.cdf(i, scale=40) 
  lista_probs.append(prob)
  n_prob.append(i)

data = {'n':n_prob,'Probabilidade':lista_probs}
df = pd.DataFrame(data)

fig = px.line(df, x='n', y='Probabilidade', markers=True,template='ggplot2',title='<b> Função de Distribuição Acumulada: lambda = 40')
fig.show()

R

Código

dexp( 2, rate=1/4 )

[1] 0,1516327

Código

qexp( p=0.75, rate=1/4, lower.tail=T )

[1] 5,545177

Código

labels <- c("rate = .5", "rate = 1", "rate = 1.5")
colors <- c("red", "blue", "darkgreen")

curve(dexp(x, rate = .5), from=0, to=10, col='blue')
curve(dexp(x, rate = 1), from=0, to=10, col='red', add=TRUE)
curve(dexp(x, rate = 1.5), from=0, to=10, col='darkgreen', add=TRUE)

legend("topright", inset=.05, title="Distributions",
  labels, lwd=2, lty=c(1, 1, 1), col=colors)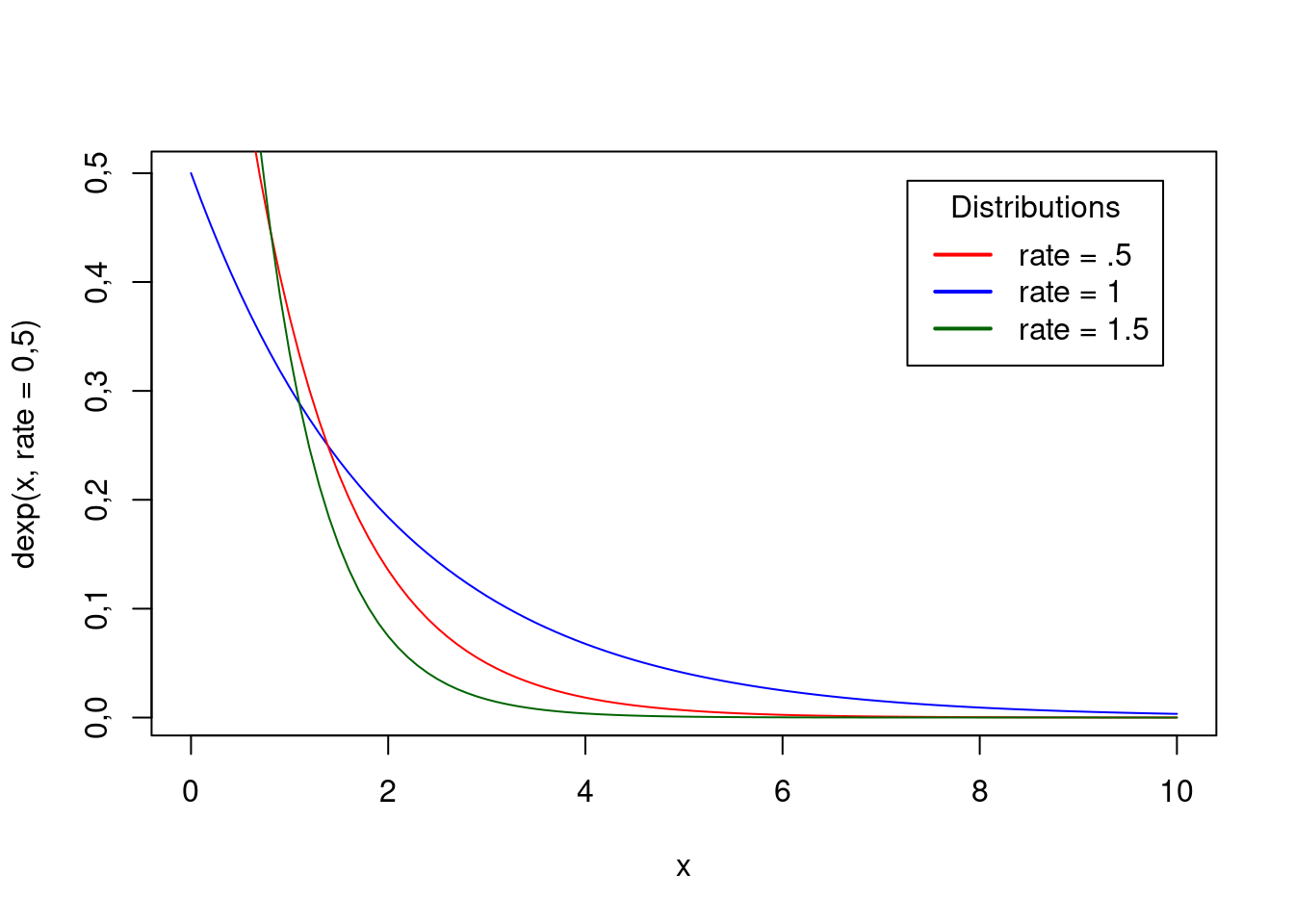

Distribuição T

A distribuição t é uma distribuição de probabilidade semelhante à distribuição normal, porém com caudas mais “grossas”. Isso porque mais valores nesta distribuição estão localizados nas extremidades das caudas do que no centro, quando a comparamos com a distribuição normal.

Sobre os testes t, eles são usados quando é necessário comparar médias. Abaixo veremos exemplos sobre como obter p-valores, a partir de um valor hipotético da estatística de teste.

Python

Para gerarmos uma amostra da distribuição t, podemos usar a função “t.rvs”. Os parâmetros que ela recebe são os graus de liberdade e tamanho da amostra (6 e 10, respectivamente, no exemplo).

Código

amostra_t=t.rvs(df=6, size=10)
amostra_t

array([-0.46425243, -0.43404586, -1.52011751, -2.07678607, -0.11229579,
       -0.11445089, -0.50848308, -0.53675386, -0.27816205,  0.61669699])

Suponha que realizamos um teste de hipótese unilateral e acabemos com uma estatística de teste de -1,5 e graus de liberdade = 10.

Podemos usar a seguinte sintaxe para calcular o p-valor que corresponde a esta estatística de teste:

Código

t.cdf(x=-1.5, df=10)

0.08225366322272008

Suponha que realizamos um teste de hipótese bicaudal e acabamos com uma estatística de teste de 2,14 e 20 graus de liberdade.

Podemos usar a seguinte sintaxe para calcular o p-valor que corresponde a esta estatística de teste:

Código

(1 - t.cdf (x=2.14, df=20)) * 2

0.04486555082549959

Abaixo, com o auxílio da biblioteca do matplotlib, plotamos a distribuição normal e T, com um grau de liberdade:

Código

# Distribuição Normal
x = np.linspace(-4, 4, 500)
y = stats.norm.pdf(x)

# Distribuição T 
df = 1
y_t = stats.t.pdf(x, df)

plt.ylabel('Densidade de Probabilidade')
plt.xlabel('Desvio Padrão')
plt.plot(x, y, color='blue', label='Normal')
plt.plot(x, y_t, color='green', label=f'T, df={df}')
plt.legend()

sns.set_context('notebook')
sns.despine()
plt.show()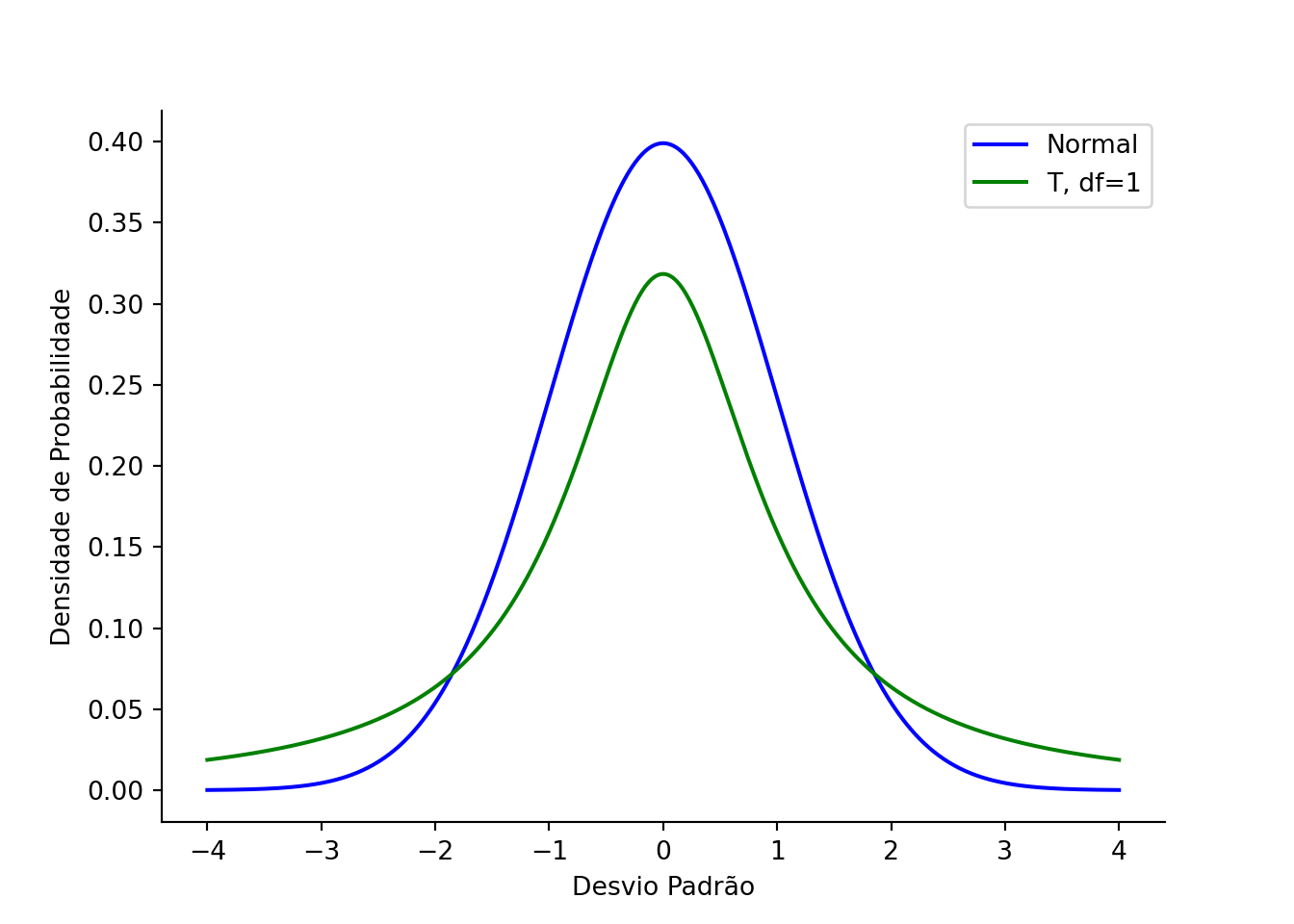

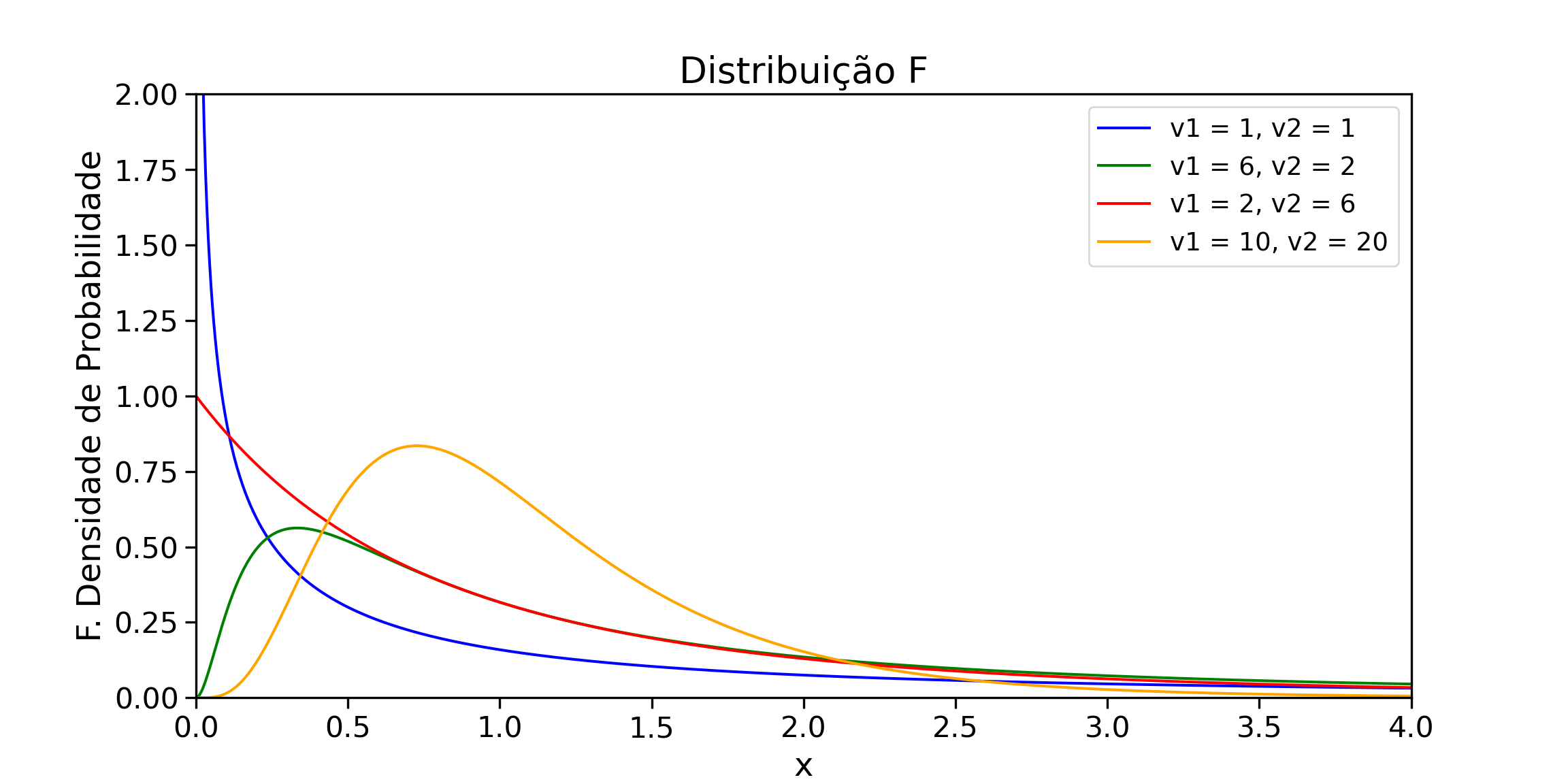
R

Código

curve(dt(x, df=10), from=-4, to=4)

Distribuição F

A distribuição F foi desenvolvida por Fisher para estudar o comportamento de duas variâncias de amostras aleatórias, retiradas de duas populações normais independentes. Em problemas aplicados, podemos estar interessados ​​em saber se as variâncias populacionais são iguais ou não, com base na resposta das amostras aleatórias.

• À medida que os graus de liberdade aumentam , a distribuição começa a convergir para uma distribuição normal;

• A distribuição geralmente é assimétrica à direita com caudas pesadas;

• É sempre positivo e contínuo.

Estas afirmações estão evidenciadas abaixo:

Python

Código

x = np.linspace(0, 4.5, 1000)
# Distribuição F   
f1 = f(1, 1, 0)
f2 = f(6, 2, 0)
f3 = f(2, 6, 0)
f4 = f(10, 20, 0)
# plot Distribuição F
plt.figure(figsize=(12, 6))
plt.plot(x, f1.pdf(x), label = 'v1 = 1, v2 = 1', color = 'blue')
plt.plot(x, f2.pdf(x), label = 'v1 = 6, v2 = 2', color = 'green')
plt.plot(x, f3.pdf(x), label = 'v1 = 2, v2 = 6', color = 'red')
plt.plot(x, f4.pdf(x), label = 'v1 = 10, v2 = 20', color = 'orange')
plt.xlim(0, 4)

(0.0, 4.0)

Código

plt.ylim(0.0, 2)

(0.0, 2.0)

Código

plt.xticks(fontsize=16)

(array([0. , 0.5, 1. , 1.5, 2. , 2.5, 3. , 3.5, 4. ]), [Text(0.0, 0, '0.0'), Text(0.5, 0, '0.5'), Text(1.0, 0, '1.0'), Text(1.5, 0, '1.5'), Text(2.0, 0, '2.0'), Text(2.5, 0, '2.5'), Text(3.0, 0, '3.0'), Text(3.5, 0, '3.5'), Text(4.0, 0, '4.0')])

Código

plt.yticks(fontsize=16)

(array([0.  , 0.25, 0.5 , 0.75, 1.  , 1.25, 1.5 , 1.75, 2.  ]), [Text(0, 0.0, '0.00'), Text(0, 0.25, '0.25'), Text(0, 0.5, '0.50'), Text(0, 0.75, '0.75'), Text(0, 1.0, '1.00'), Text(0, 1.25, '1.25'), Text(0, 1.5, '1.50'), Text(0, 1.75, '1.75'), Text(0, 2.0, '2.00')])

Código

plt.xlabel('x', fontsize=18)
plt.ylabel('F. Densidade de Probabilidade', fontsize=18)
plt.title("Distribuição F",fontsize=20)
plt.legend(fontsize=14)
plt.show()

R

Código

x_df <- seq(0, 20, by = 0.1)       

y_df <- df(x_df, df1 = 3, df2 = 5)

plot(y_df)